El logaritmo de un número —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 elevado a la potencia 3: 1000 = 103 = 10×10×10.
De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponenciación de la base del logaritmo.
Para representar la operación de logaritmo en una determinada base se escribe la abreviatura log y como subíndice la base y después el número resultante del que deseamos hallar el logaritmo. Por ejemplo, 35=243 luego log3243=5. Cuando se sobreentiende la base, se puede omitir.
Definición
El logaritmo en base a de un número C es el exponente al cual hay que elevar la base para obtener dicho número.
(esto se lee como: logaritmo en base a de C es igual a b; si y sólo si a elevado a la b es igual a C)
Para que esta definición sea válida, no todas las bases y números son posibles. La base a tiene que ser positiva y distinta de 1, luego a> 0 y a ≠ 1, C tiene que ser un número positivo C > 0 y b puede ser cualquier número real (b ∈ R).
Para aclarar el concepto, podríamos decir que logaritmo es solo otra forma de expresar la potenciación, como en este ejemplo:
Que leeremos: logaritmo de 64 en base 8 es igual a 2.
Esto significa que una potencia se puede expresar como logaritmo y un logaritmo se puede expresar como potencia.
El gráfico siguiente nos muestra el nombre que recibe cada uno de los elementos de una potencia al expresarla como logaritmo:
Ejemplos:
Propiedades de los logaritmos
-
- 1. El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
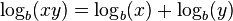
En realidad la tercera y cuarta identidad son equivalentes, sin más que hacer:
5. Cambio de base: El logaritmo en base a de un número se puede obtener a partir de logaritmos en otra base
Ejemplo:
- No existe el logaritmo de un número con base negativa.
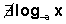
- No existe el logaritmo de un número negativo.
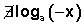
- No existe el logaritmo de cero.
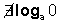
- El logaritmo de 1 es cero.
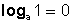
- El logaritmo de a en base a es uno.
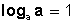
Logaritmos decimales:
Son los que tienen base 10. Se representan por log (C) (la base 10 no se escribe).
Logaritmos neperianos o naturales:
Son los que tienen base e. Se representan por ln (C) o L(C) (en este caso la base e tampoco se escribe, basta con que aparezca ln).
Algunos ejemplos de logaritmos neperianos son:
ln 1 = 0; puesto que e0 = 1
ln e2 = 2; puesto que e2 = e2
ln e−1 = −1; puesto que e−1 = e−1
El número e tiene gran importancia en las Matemáticas. No es racional (no es cociente de dos números enteros) y su valor, con seis cifras decimales, es
e = 2,718281...
log 4 64 + log 4 1 = log 4 (64*1) = log 4 64 = 3











Hallar el valor de y:












EJERCICIOS RESUELTOS
1. log 4 64 + log 4 1 =
3 + 0 = 3
Alternativamente, podríamos resolverlo usando la Propiedad del logaritmo de un producto, así:
log 4 64 + log 4 1 = log 4 (64*1) = log 4 64 = 3
2. log 5 + log 20 =
= log (5*20) (aplicando la Propiedad del logaritmo de un producto)
= log 100
= 2
3. log 5 25 - log 5 5 =
2 - 1 = 1
Tambíén se pudo resolver usando la propiedad del logaritmo de un cociente:
log 5 25 - log 5 5 = log 5 (25 / 5) = log 5 5 = 1
4. log 0,1 - log 0,01 =
-1 - (-2) = 1
Ahora resolvamoslo usando la propiedad del logaritmo de un cociente:
log 0,1 - log 0,01 = log (0,1 / 0,01) = log10 = 1
5. 

6. 
7. 

8. 

9. 
10. log 4 64 + log 8 64 =
3 + 2 = 5
11. log 32 / log 2 =
=1,5051 / (0,3010)
= 5
12. log 2 - log 0,2 =
= log (2 / 0,2) (aplicando la Propiedad del logaritmo de un cociente)
= log 10
= 1
Hallar el valor de x:
13. log 2 x = - 3
x = 2 -3
x = 1 / 23
x = 1 / 8
14. log 6 [ 4 ( x - 1 ) ] = 2
log 6 4 + log 6 ( x - 1 ) = 2 (Aplicamos la Propiedad del Cambio de base):
(log 10 4 / log 10 6) + log 6 ( x - 1 ) = 2
= (0,6020 / 0,7781) + log 6 ( x - 1 ) = 2
=0,7737 + log 6 ( x - 1 ) = 2
= log 6 ( x - 1 ) = 2 - 0,7737
= log 6 ( x - 1 ) = 1,22629
( x - 1 ) = 61,22629
x - 1 = 9
x = 9 + 1
x = 10
15. log 7 x = 3
x = 73
x = 343
16. 

17. 

18. 
19. log x 125 = 3
x3 = 125
x = 5
20. log x 25 = - 2
x-2 = 25
x2 = 1 / 25
x = 1 / 5
21. log 2 x + 3 81 = 2
(2x + 3)2 = 81 sacamos raiz cuadrada a ambos lados
2x + 3 = 9
2x = 9 - 3
2x = 6
x = 3
22. 

23. 


24. log 8 [ 2 ( x 3 + 5 ) ] = 2
log 8 2 + log 8 ( x 3 + 5 ) ] = 2 (Aplicamos la Propiedad del Cambio de base):
(log 10 2 / log 10 8) + log 8 ( x 3 + 5 ) ] = 2
0,33333 + log 8 ( x 3 + 5 ) ] = 2
25. log 8 ( x 3 + 5 ) ] = 2 - 0,33333
log 8 ( x3 + 5 ) ] = 1,66667
( x3 + 5 ) = 81,66667
x3 + 5 = 32
x3 = 32 - 5
x3 = 27
x = 3
26. 
Hallar el valor de y:
27. 
28. 

29. 

30. 
31. 

32. 
33. 
34. 
= 




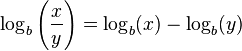
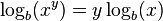
![\!\, \log_b(\sqrt[y]{x}) = \frac{\log_b(x)}{y} \,](http://upload.wikimedia.org/math/e/3/2/e32fd943d2fc67a7033c9d67046522e3.png)
![\!\, \sqrt[y]{x} = x^\frac{1}{y} \,](http://upload.wikimedia.org/math/e/7/d/e7d30a4c68d2e42f12b4fd6bc4417864.png)


muchas gracias :D
ResponderEliminarF
ResponderEliminaren una imagen me resumio lo que intente comprender en una semana :v
ResponderEliminar