La potenciación es una multiplicación de varios factores iguales, al igual que la multiplicación es una suma de varios sumandos iguales. La potenciación se considera una multiplicación abreviada.
En la nomenclatura de la potenciación se diferencian dos partes, la base y el exponente, que se escribe en forma de superíndice. El exponente determina la cantidad de veces que la base se multiplica por sí misma.
Definición
Se llama potencia a una expresión de la forma an
, donde a es la base y n es el exponente. Su definición varía según el conjunto
numérico al que pertenezca el exponente.
Por ejemplo:
En general:
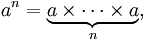
Normalmente, las potencias con base 10, por la cantidad que represente el exponente, esa será la cantidad de ceros en el resultado. El resto de la bases, para sacar el resultado el número se multiplica por sí mismo cuantas veces indique el exponente.
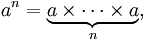
Normalmente, las potencias con base 10, por la cantidad que represente el exponente, esa será la cantidad de ceros en el resultado. El resto de la bases, para sacar el resultado el número se multiplica por sí mismo cuantas veces indique el exponente.
Propiedades de la potenciación
Las propiedades de la potenciación son las que permiten resolver por diferentes métodos una potencia. Estas son:
Potencia de exponente 0
Toda potencia de exponente 0 y base distinta de 0 es igual a 1.
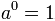 si se cumple que
si se cumple que 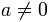
30= 1
200=1
Potencia de exponente 1
Toda potencia de exponente 1 es igual a la base
Ejemplo:
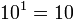
Producto de potencias de igual base
Para el producto de dos o más potencias de igual base se coloca la misma base y se suman los exponentes.
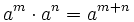
Ejemplos:
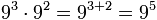
52 * 58 = 52+8 = 510
112 * 113 = 112+3 = 115
284 * 289 * 287 = 284+9+7 = 2820
9-2 * 93 * 96 = 9-2+3+6 = 97

División de potencias de igual base
En la división de dos potencias de igual base se coloca la misma base y se restan los exponentes.
Ejemplo:
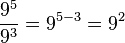 = 81
= 81
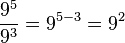 = 81
= 815 8 : 5 3 = 5 8-3 = 55 = 25 (entiéndase : como dividido entre)
49 : 46 = 5 9-6 = 43 = 64
(-7)3 : (-7)6 = (-5)3-6 = -7-3 = 1 / -73 = 1 / -343
Potencia de un producto(-7)3 : (-7)6 = (-5)3-6 = -7-3 = 1 / -73 = 1 / -343
La potencia de un producto de base (a·b) y de exponente "n" es igual a la potencia "a" a la "n" por "b" a la "n". Cada base se multiplica por el exponente.
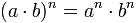
Si la base a tiene inverso aditivo, indicado mediante signo negativo -a, entonces se tiene la regla:
 si n es par. si n es par. si n es impar. si n es impar. |
Si la base a tiene inverso multiplicativo c, es decir c·a = 1 o que  , entonces este se denota por
, entonces este se denota por  y el exponente se puede ampliar a todos los números enteros:
y el exponente se puede ampliar a todos los números enteros:
 , entonces este se denota por
, entonces este se denota por  y el exponente se puede ampliar a todos los números enteros:
y el exponente se puede ampliar a todos los números enteros:(2)
- Observación

Ejemplos:
Potencia de un cociente
La potencia de un cociente es igual al cociente de cada uno de los números elevado al mismo exponente.
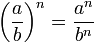
Ejemplos:
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a y cuyo exponente es el producto de ambos exponentes (la misma base y se multiplican los exponentes):
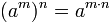
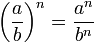
Ejemplos:
Potencia de una potencia
La potencia de una potencia de base a es igual a la potencia de base a y cuyo exponente es el producto de ambos exponentes (la misma base y se multiplican los exponentes):
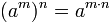
Debido a esto, la notación  se reserva para significar
se reserva para significar 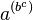 ya que
ya que  se puede escribir sencillamente como
se puede escribir sencillamente como  .
.
Ejemplos:
 se reserva para significar
se reserva para significar 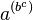 ya que
ya que  se puede escribir sencillamente como
se puede escribir sencillamente como  .
.Ejemplos:
Propiedad distributiva
La potenciación es distributiva con respecto a la multiplicación y a la división, pero no lo es con respecto a la suma ni a la resta.
Distributiva con respecto a la multiplicación y división:
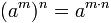
No es distributiva con respecto a la adición y sustracción:
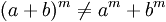
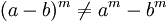
Ejemplos:
Propiedad conmutativa
La propiedad conmutativa no se cumple para la potenciación, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes.
En general:
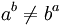
Propiedad asociativa
La propiedad asociativa no se cumple para la potenciación.
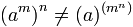
Potencia de base 10
Para las potencias con base 10 y exponente entero, el efecto será desplazar la coma decimal tantas posiciones como indique el exponente, hacia la izquierda si el exponente es negativo, o hacia la derecha si el exponente es positivo.
Ejemplos:
Potencia de exponente fraccionario
Es una potencia que tiene su exponente en forma de fracción, y en la que se cumple que

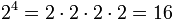







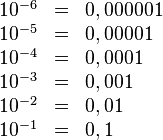
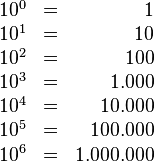
me encanta la matemática me instruye y me divierte
ResponderEliminarno joda me mandaro a hacer esa mierda y en tendi un coño noja matematica en una mierda como materia
ResponderEliminarsi, pero sin ser grosero
Eliminarmuy bueno, me entretiene y desarrolla mas mis neuronas
ResponderEliminarMe ayudó mucho
ResponderEliminar