Cálculo del MCD
Los dos métodos más utilizados para el cálculo del máximo común divisor de dos números son:
Forma larga de calcular el MCD
Para calcularlo. De los números que vayas a sacar el máximo común divisor, se ponen uno debajo del otro, se sacan todos los divisores de los dos números y el máximo que se repita es el máximo común divisor (M.C.D.Ejemplo: Calcular el MCD de 20 y 10:
Ejemplo: Calcular el MCD de 18 y 24
Cálculo del MCD Por descomposición en factores primos
El máximo común divisor de dos números puede calcularse determinando la descomposición en factores primos de los dos números y tomando los factores comunes elevados a la menor potencia, el producto de los cuales será el mcd.
Ejemplo: para calcular el máximo común divisor de 48 y de 60 se obtiene de su factorización en factores primos.
|
|
|
El MCD son los factores comunes con su menor exponente, esto es:
En la práctica, este método solo es operativo para números pequeños tomando en general demasiado tiempo calcular la descomposición en factores primos de dos números cualquiera.
Esto también podríamos haberlo hecho poniendo uno frente al otro los números y luego vamos calculando los factores primos que sean comunes a todos los números. Siguiendo con el mismo ejemplo tendríamos lo siguiente:
veamos otro ejemplo:
Hallar el m. c. d. de: 72, 108 y 60.
Usando el algoritmo de Euclides
Un método más eficiente es el algoritmo de Euclides, que utiliza el algoritmo de la división junto al hecho que el mcd de dos números también divide al resto obtenido de dividir el mayor entre el más pequeño. Por ejemplo, si se divide 60 entre 48 dando un cociente de 1 y un resto de 12, el mcd será por tanto divisor de 12. Después se divide 48 entre 12 dando un resto de 0, lo que significa que 12 es el mcd. Formalmente puede describirse como:
Ejemplo:
Hallar el m. c. d. de: 250 y, 100
Aplicaciones
El mcd se utiliza para simplificar fracciones. Por ejemplo, para simplificar la fracción 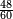 se calcula primero el mcd(60, 48) = 12, dividiéndose el numerador y el denominador de la fracción inicial por 12 para obtener la fracción simplificada
se calcula primero el mcd(60, 48) = 12, dividiéndose el numerador y el denominador de la fracción inicial por 12 para obtener la fracción simplificada  .
.
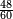 se calcula primero el mcd(60, 48) = 12, dividiéndose el numerador y el denominador de la fracción inicial por 12 para obtener la fracción simplificada
se calcula primero el mcd(60, 48) = 12, dividiéndose el numerador y el denominador de la fracción inicial por 12 para obtener la fracción simplificada  .
.
El mcd también se utiliza para calcular el mínimo común múltiplo de dos números. En efecto, el producto de los dos números es igual al producto de su máximo común divisor por su mínimo común múltiplo. Así, para calcular el mínimo común múltiplo de 48 y de 60, calculamos primero su mcd, 12, siendo su mínimo común múltiplo  .
.
 .
.




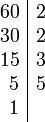
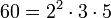




necesito que me enseña el minimo comun divisor y maximo comun divisor po favor
ResponderEliminarMe piden q encuentre el MCD y MCM de 15 y 42,como lo hago??
ResponderEliminarEn los divisores de 20 falto el 4
ResponderEliminar345688865421
Eliminarhola
ResponderEliminarHola xd
Eliminar