MATEMATICAS PARA EL BACHILLERATO: NUMEROS IRRACIONALES

En matemáticas, un número irracional es un número que no puede ser expresado como una fracción

\frac{m}{n}

, donde

m

n

son enteros y

n

es diferente de cero.
Es cualquier número real que no es racional.

Debido a ello, los números irracionales más conocidos son identificados mediante símbolos especiales; los tres principales son los siguientes:

$\pi$ (Número "pi" 3,14159...): razón entre la longitud de una circunferencia y su diámetro.
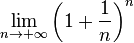
e (Número "e" 2,7182...): $\lim _{n \to +\infty} \left( 1 + \frac {1}{n}\right) ^{n}$
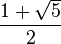
$\Phi$ (Número "áureo" o Razón de oro 1,6180...): $\frac{1 + \sqrt{5}}{2}$
las soluciones reales de x² - 3 = 0; de x⁵ -7 = 0; de x³ = 11; 3^x = 5; sen 7º, etc